Choose your operating system:
Windows
macOS
Linux
The Groom system is designed to handle hair strands from imported groom Alembic (.abc) files. However, for scalability purposes, it also supports alternative geometry representations using cards and meshes. All of these geometric representations are managed within a single asset and component for ease of setup.
The Groom Asset Editor manages most of the aspects of your groom, enabling you to modify various parts of the groom for how it's rendered, how it handles physics simulation, creating and managing levels of detail (LODs), and much more.
Opening the Groom Asset Editor
The Groom Asset Editor is opened from the Content Browser by double-clicking any Groom Asset , or through the right-click context menu of a Groom Asset .

Groom Asset Editor Interface
The Groom Asset Editor is comprised of these regions:

-
Viewport Display Options : Includes viewport options, view perspectives, view modes, debug views, and level of detail visualization.
-
Viewport : Displays the groom asset with its assigned materials, level of details, and physics representation.
-
Details Panels : Includes
Viewport Display Options
The Viewport Display Options toolbar provides basic rendering and visualization options.

Viewport Options
The Viewport Options dropdown menu provides basic rendering options within the viewport. You can toggle real-time mode, change the field of view, and set the screen percentage for supersampling.
These options, and more, are accessed using the dropdown arrow in the viewport display options toolbar.

Perspectives
The Perspectives dropdown provides perspective and orthographic views; a perspective view that's a 3D window into the level, and orthographic views that are 2D viewports that look down on of the main XYZ axes.

View Modes
The View Modes dropdown provides a number of visualization options common to all editor viewports, such as lighting, optimization, materials, and exposure value control for the viewport.

To learn more about these visualization view modes, see Viewport Basics .
Show
The Show dropdown provides Groom Asset Editor specific visualization options to help you see the type of data being processed in your scene, as well as diagnose errors or unexpected results for this groom.

|
Property |
Description |
|---|---|
|
Guide |
Displays the guides used for simulation. |
|
Guide Influence |
Shows simulation clumps (all the strands influenced by one guide) in color visualization. |
|
UV |
Displays the UV along each strand. |
|
Root UV |
Displays the UV at the root of each strand. |
|
Root UDIM |
Displays the UDIM at the root of each strand. |
|
Dimension |
Displays the width/length variations of each strand. |
|
Seed |
Displays (in color) the random seed used per strand. |
|
Radius Variation |
Shows (in color) the size of the strands. Blue represents thinner strands. Yellow represents thicker strands. |
|
Base Color |
Displays the base color stored per vertex. If base color is not exported from your modeling application with your groom, the strands will appear black. |
|
Roughness |
Displays the roughness stored per vertex. If the roughness is not exported from your modeling application with your groom, the strands will appear black. |
|
Vis Cluster |
Shows clusters of hair used for culling and level of detail purposes. |
|
Cards Guide |
These are some example visualizations from the Show dropdown.
|
|
|
|
|
|---|---|---|---|
|
Guides |
Seed |
Radius Variation |
Base Color |
LODs
The LODs dropdown enables you to visualize levels of detail within the viewport automatically or by specifying a particular level.
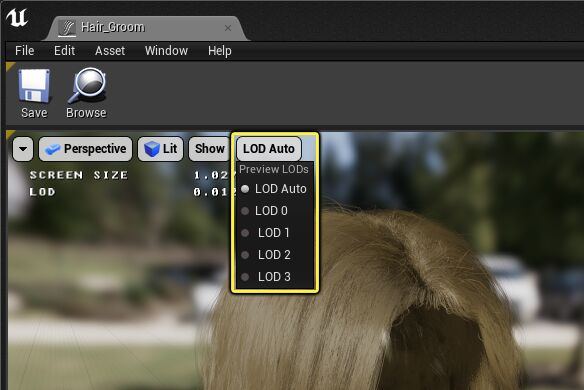
Switch between LODs automatically based on the options specified in the Level of Detail panel when using the LODs Auto option. This option automatically switches LODs based on their screen size in the viewport. Alternatively, use the dropdown to select from the available levels of detail that have already been generated to see them represented regardless of screen size.
Viewport
The Viewport is where you can view your imported Groom Asset with changes made in its different details panels, and use different visualization and debug view modes to inspect your groom.
For additional information about viewport navigation and visualization techniques, see Editor Viewports .
Details Panels
The Groom Asset Editor contains several Details panels which control a variety of attributes related to your groom.
Explore the panels below to learn about the attributes, properties, and options available:
Level of Detail
The Level of Detail (LOD) panel ctonrols the decimation of the groom's individual levels of detail. This includes controlling at what visible screen size the LOD should change and what type of geometry it should use (strands, mesh, or cards) for representation.

|
Property |
Description |
|
|---|---|---|
|
LOD [N] |
||
|
Curve Decimation |
Decimates the groom by reducing the number of strands. The removed strands are chosen randomly from the groom's imported strands. |
|
|
Vertex Decimation |
Decimates the groom by removing vertices on strands. |
|
|
Angular Threshold |
Defines the maximal angle value of two consecutive strands' segments for removing a vertex. Higher values mean more decimation. |
|
|
Screen Size |
Defines the screen size below which this LOD will be enabled. |
|
|
Thickness Scale |
Increases the strand thickness compensating for the loss of a strands curve. The Thickness Scale adjust an automatic scaling value that is computed. |
|
|
Visible |
Toggles the visibility of this LOD. |
|
|
Geometry Type |
Sets what type of geometry will be used to represent this level of detail. Choose between the following:
|
|
|
Cluster World Size |
Defines the average size (in world space) of a hair cluster. A groom is divided into a set of clusters for fine grain level of detail selection and culling. |
|
|
Cluster Screen Size Scale |
Scales the projected screen of a cluster to bias its level of detail selection. |
|
|
LOD |
||
|
LOD Selection Type |
Set whether the LOD selection should happen on the CPU or the GPU . When CPU is selected, the strands LODing is coarser but allows for all types of geometrical representation (strands, cards, and meshes). When GPU is selected, LODing is more fine grain but only supports strand geometry. |
|
|
Minimum LOD |
Specify the minimum LOD of detail to cook for all platforms, or specify minimum LODs for individual platforms by adding them using the Plus button. |
|
|
Disable Below Min LOD Stripping |
Set a flag to override the removal of LODs below the Minimum LOD set for all platforms, or specify platforms by adding them using the Plus button. |
|
To preview the various LOD in the editor viewport, click on the LOD Auto button within the viewport and select the desired LOD:
|
|
|
|---|---|
|
Higher Detail LOD |
Lower Detail Imported Mesh LOD |
Interpolation
The Interpolation panel modifies some of the properties set during initial import of the groom.

|
Property |
Description |
|
|---|---|---|
|
Hair Group |
||
|
Curve Decimation |
Decimates the groom by reducing the number of strands. The removed strands are chosen randomly from the groom's imported strands. |
|
|
Vertex Decimation |
Decimates the groom by removing vertices on strands. |
|
|
Override Guides |
When enabled, overrides the imported guides by selecting a subset of strands used as a guide. |
|
|
Hair to Guide Density |
Defines the ratio of strands used as guides. |
|
|
Interpolation Quality |
Defines the quality of the interpolation when interpolating Guides motions onto the strands. |
|
|
Interpolation Distance |
Defines metric used for pairing guides and strands together. |
|
|
Randomize Guide |
When enabled, the guides used for interpolation are slightly randomized to break up clumps that can happen. |
|
|
User Unique Guide |
When enabled, a single guide is used for motion interpolation. |
|
|
Interpolation |
||
|
RBF Interpolation |
When enabled, the Radial Basis Function (RBF) is used for interpolation instead of the local skin rigid transform. |
|
|
Hair Interpolation Type |
Select the type of interpolation to use when the groom is bound to a Skeletal Mesh:
|
|
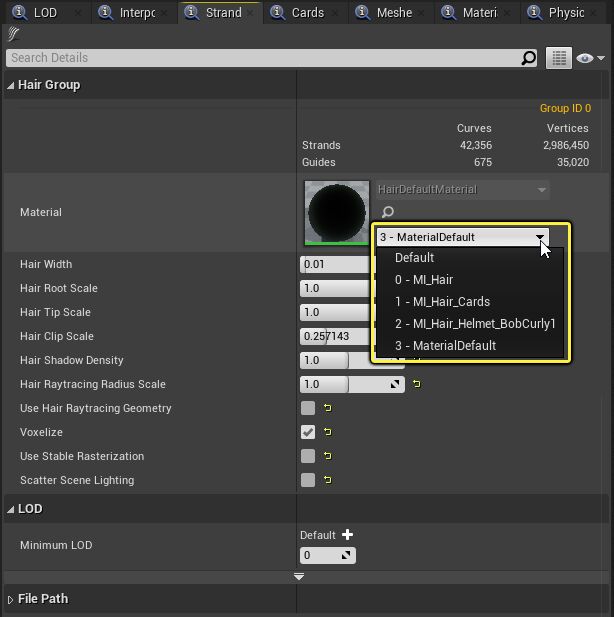
Strands
The Strands panel controls various rendering properties related to the strands geometry of the groom. You can set your material, change key properties of the strands of the hair, such as width, root and tip scale, and enable ray tracing for the groom.

|
Property |
Description |
|---|---|
|
Material |
The material used for the cards representation LODs. |
|
Hair Width |
Changes the size of the hair strands. This value corresponds to the width of the largest strand with the default value coming from the imported groom. |
|
Hair Root Scale |
Scales the width of the strand starting with the strand's root and fading down towards the tip. |
|
Hair Tip Scale |
Scales the width of the strand from the strand's tip and fading down towards the root. |
|
Hair Clip Scale (DEPRECATED) |
Clip the hair at a certain distance from the strand's root. This property is deprecated and will be removed in a future release of Unreal Engine. |
|
Hair Shadow Density |
Scales the hair density making shadow and transmission lighter or stronger uniformly over the groom. |
|
Hair Raytracing Radius Scale |
Scales the strand's width when raytraced shadowing is used. |
|
Voxelize |
When enabled, hair strands are voxelized to provide more accurate lighting computation. |
|
Use Stable Rasterization |
When enabled, the strands are less noisy but can appear a little bit thicker. |
|
Scatter Scene Lighting |
When enabled, the strands use the underlying scene lighting as a source light. This property is intended for really short hair, like peach fuzz. |
Cards
The Cards panel is where you set up your cards' geometry, textures, and specify whether the engine should generate cards procedurally or use imported ones.

|
Property |
Description |
|
|---|---|---|
|
Material |
The assigned material used for the Cards representation LODs. |
|
|
Source Type |
Choose the type of cards to use:
|
|
|
Procedural Mesh |
The mesh reference for the card geometry. |
|
|
Imported Mesh |
The mesh reference for the card geometry. |
|
|
Procedural Settings (See Below) |
||
|
Textures |
||
|
Depth Texture |
The depth texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Coverage Texture |
The coverage texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Tangent Texture |
The tangent texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Attribute Texture |
The attribute texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Auxiliary Data Texture |
The auxilliary texture enables user data to be transferred for the Cards Asset. It is an optional texture that when set, the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Group Index |
The group index on which this card's geometry will be mapped to |
|
|
LOD Index |
The LOD index at which this cards asset should be used. |
|
Procedural Generation
This feature is experimental. Output results can vary widely depending on the complexity of your grooms.
The Procedural selection generates cards from your strands in your groom. You can specify Geometry and Texture properties that determine how the cards are generated for your groom.

|
Property |
Description |
|
|---|---|---|
|
Geometry Setting |
||
|
Generation Type |
Choose whether to use guides or strands for card generation. When strands are selected, a random selection will be used for card generation. |
|
|
Cards Count |
Defines how many cards are generated when Generation Type is set to Cards Count . |
|
|
Cluster Type |
Defines how clumps are formed to generate cards. Choose between High and Low. High creates more well defined clumps but is slower to process. |
|
|
Min Segment Length |
Defines the minimum length between two consecutive card segments. |
|
|
Angular Threshold |
Defines the maximal angle value of two consecutive card segments. Higher values reduce the geometrical complexity of the cards decimation. |
|
|
Min Cards Length |
Cards having length smaller than this threshold are removed. |
|
|
Max Cards Length |
Cards having length larger than this threshold are removed. |
|
|
Texture Settings |
||
|
Atlas Max Resolution |
The maximum atlas resolution of the generated cards atlas. This value is only a suggestion for the card generator and is not enforced. |
|
|
Pixel Per Centimeters |
Sets the pixel density (or precision) for generating the cards atlas. |
|
|
Length Texture Count |
The number of clumps variations to be generated. |
|
Generating Procedural Cards
Generate a procedural Cards Asset using the following steps:
-
Set the Source Type to Procedural using the dropdown menu.
-
Set the Group Index and the LOD Index for which the cards should be generated. For example, if you want LOD 2 to use cards instead of strands, you would use 2 for the indices.
-
Under the Source Type dropdown menu, press the Refresh button to generate the Cards Asset.
-
Under the Source Type dropdown menu, press the Save button to save and reload the Cards Asset.
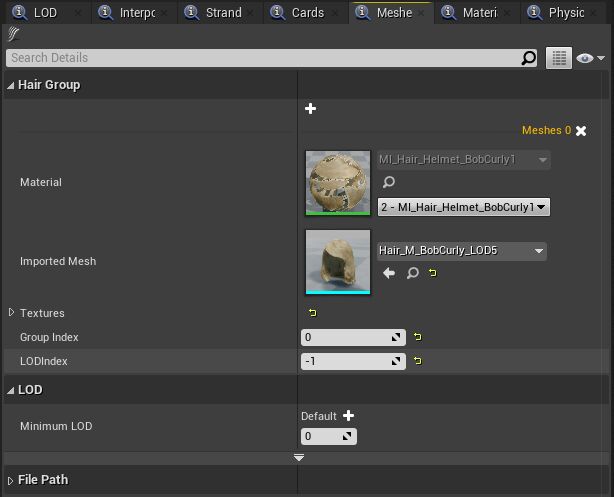
Meshes
The meshes panel manages the mesh geometry used for LODs in a Groom Asset. This panel lists all mesh geometry, but all listed geometry is not necessarily used.
|
Property |
Description |
|
|---|---|---|
|
Material |
The assigned material used for the Cards representation LODs. |
|
|
Imported Mesh |
The assigned mesh geometry to be referenced. |
|
|
Textures |
||
|
Depth Texture |
The depth texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributesnode in the Material Editor. |
|
|
Coverage Texture |
The coverage texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Tangent Texture |
The tangent texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Attribute Texture |
The attribute texture used for the cards asset. This texture is optional, but when set the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Auxiliary Data Texture |
The auxilliary texture enables user data to be transferred for the Cards Asset. It is an optional texture that when set, the value is forwarded to the Hair Attributes node in the Material Editor. |
|
|
Group Index |
The group index that this card's geometry will be mapped to. |
|
|
LOD Index |
The LOD index at which this card asset should be used. |
|
|
LOD |
||
|
Minimum LOD |
Specify the minimum LOD of detail to cook for all platforms, or specify specific minimums for individual platforms by adding them using the Plus button. |
|
Materials
The Materials panel defines materials that can be used by the Groom Asset.
Use the Add ( + ) button to add a new Material reference. Use the Slot Name to give the material a name, otherwise it'll use the default name of the material that is assigned.

The
Material
slots found in the
Strands
,
Meshes
, and
Cards
panels lets you select from the referenced materials list.
Physics
The Physics panel provides settings to enable physics simulation, and modifying motion behavior of grooms.

|
Property |
Description |
|
|---|---|---|
|
Solver Settings |
||
|
Enable Simulation |
Enables physics simulation for the groom asset. |
|
|
Niagara Solver |
Select the Niagara solver to be used for simulation. Choose from Groom Rods , Groom Springs , and Custom Solver . |
|
|
Custom System |
Add a custom Niagara system to be used if the Niagara Solver is set to Custom Solver. |
|
|
Sub Steps |
The number of sub steps to be done per frame. The actual solver calls are done at 24 frames per second. |
|
|
Iteration Count |
The number of iterations to solve constraints with the xpbd solver. |
|
|
External Forces |
||
|
Gravity Vector |
The acceleration vector measured in cm/s2 to be used for gravity. |
|
|
Air Drag |
The coefficient between 0 and 1 to be used for air drag. |
|
|
Air Velocity |
The velocity of the surrounding air measured cm/s. |
|
|
Material Constraints: Bend Constraints |
||
|
Solve Bend |
Enables the solve of the bend constraint during the xpbd loop. |
|
|
Project Bend |
Enables the projection of the bend constraint after the xpbd loop. |
|
|
Bend Damping |
Damping applied for the bend constraint using a value between 0 and 1. |
|
|
Bend Stiffness |
The stiffness for the bend constraint in GPa. |
|
|
Stiffness Scale |
The curve determines how much the bend stiffness is scaled along each strand. The X axis range is 0,1. 0 maps to the root and 1 to the tip. |
|
|
Material Constraints: Stretch Constraints |
||
|
Solve Stretch |
Enables the solve of the stretch constraint during the xpbd loop. |
|
|
Project Stretch |
Enables the projection of the stretch constraint after the xpbd loop. |
|
|
Stretch Damping |
The damping for the stretch constraint using a value between 0 and 1. |
|
|
Stretch Stiffness |
The stiffness for the stretch constraint in GPa. |
|
|
Stiffness Scale |
The curve determines how much the stretch stiffness is scaled along each strand. The X axis range is 0,1. 0 maps to the root and 1 to the tip. |
|
|
Material Constraints: Collision Constraints |
||
|
Solve Collision |
Enables the solve of the collision constraint during the xpbd loop. |
|
|
Project Collision |
Enables the projection of the collision constraint after the xpbd loop. |
|
|
Static Friction |
The static friction used for collision against the Physics Asset. |
|
|
Kinetic Friction |
The kinetic friction used for collision against the Physics Asset. |
|
|
Strands Viscosity |
The viscosity between 0 and 1 that is used for self-collision. |
|
|
Grid Dimension |
The dimension of the grid used to compute the viscosity force. |
|
|
Collision Radius |
The radius that will be used for the collision detection against the Physics Asset. |
|
|
Radius Scale |
The curve determines how much the collision radius is scaled along each strand. The X axis range is 0,1. 0 maps to the root and 1 to the tip. |
|
|
Strands Parameters |
||
|
Strands Size |
The number of particles per guide that will be used for simulation. |
|
|
Strands Density |
The density of strands measured in g/cm3. |
|
|
Strands Smoothing |
The smoothing between 0 and 1 of the incoming guides curves for better stability. |
|
|
Strands Thickness |
The strands thickness in centimeters that will be used for mass and inertia computation. |
|
|
Thickness Scale |
The curve determines how much the strands thickness is scaled along each strand. The X axis range is 0,1. 0 maps to the root and 1 to the tip. |
|






